Music Theory For (Jazz) Guitarists

This blog is targeted at guitarists that have been playing for a while and have mastered the basics such as playing pentatonic scales and the major and minor chords and want to move on with their playing. Since I’m convinced you can only learn theory by putting it into practice, I have molded the theory around some jazz songs.

First, the introduction to some basic theory and terminology,

Introduction

First I’d like to introduce: The Octave.

Wikipedia: In music, an octave is the interval between one musical pitch and another with half or double its frequency.

Why this piece of theory? The octave is a physical phenomenon and has no cultural background. Everything that you will read below is an interpretation of the western culture of this given physics. But wherever you are in the world, an octave is an octave.

Sound is a vibration of air. The quantity of vibration is expressed in frequency (the number of vibrations per second also known as Hertz after the German physicist Hertz). When a certain tone has a frequency of 440 vibrations per second, then the octave of this tone has 880 vibrations per second. And the octave of that tone 1760 vibrations per second and the next octave… etc.

The text below is an attempt to give insight into generic music theory, focused on Jazz music and guitar. Please be aware, the theory below is not complete skips subjects here and there. This is done on purpose since music theory in general is very complex and knows an history of thousands of years (e.g. in ancient Greece, music theory rules were already defined by Pythagoras). Music theory has been part of different cultural movements, religion, new insights in physics etc. Throughout the years naming conventions were established which to our modern ears might seem to be out dated. When I wrote the piece below, I decided to give as much theory as needed to give enough understanding. I also use the archaic terms since this is the language in which musicians communicate. Regarding music theory there is an awful number of web pages, books and other resources available. You find some in my ‘links’ page.

Splitting up the octave: Scales

In western music, we make use of 12 tones: an octave is divided into 11 parts which makes our scale a 12 tone scale. Why 12 and not 13 or 513 is not so simple to explain. You have to assume this as a given in our western music history theory. You can read more about it on my other blog “Western Music – How did we end up with 12 notes?“.

All these 12 tones got a unique name. It’s a very simple name since it consists of a letter and possibly a sign. Some of the tones have 2 names, I will mention the two names now but will ignore this later on since for us it’s of no use.

The ‘names’ are:

• A
• A# or Bb
• B
• C
• C# or Db
• D
• D# or Eb
• E
• F
• F# or Gb
• G
• G# or Ab

and the next ‘name’ is A again (the octave).

To make it all confusing, in music theory we like to start not on the A but on the C. Besides that, we call a step to the next tone a half note and the step to the second next tone a whole note .

So from the C to the C# (of Db) is a half note, from the C to the D is a full note. The distances between two (random) notes (like a half or a full note) is called an interval.

Based upon these twelve tones we can make scales. You just pick a number of tones from your collection of 12 tones, et volia, you have a scale (practically it doesn’t work like this but since there are numerous scale combinations based upon these 12 notes you sometimes think that any random sequence is a specific scale).

Let’s say, you don’t like all these #’s and b’s, so you pick only the notes that have only a one letter name. Then you get (starting from C as we like to do in music theory):

• C-D-E-F-G-A-B

If you would ask a piano player to play this note sequence, he/she would only play the white keys and you would hear a very famous ‘melody’:

• Do-Re-Mi-Fa-Sol-La-Ti-Do <do-re-mi>

Of course, this is no coincidence. Centuries of music theory, experiments and disputes are behind this simple tone sequence. That’s too complicated for now.

What’s important now is to see what ‘intervals’ are used. So based upon our 12 notes, what distances (intervals) are there between the notes to get our 7 tone scale?

• C-WHOLE-D-WHOLE-E-HALF-F-WHOLE-G-WHOLE-A-WHOLE-B-HALF-C

And this is vital for playing guitar. HALF means move one fret, FULL means move two frets (can be both up and down the fretboard). So the formula for this scale is:

• ‘WHOLE-WHOLE-HALF-WHOLE-WHOLE-WHOLE-HALF’

Let’s put this formula into practice. But this time I don’t start from the C in our 12 tone but I start from the E. We get the following scale:

• E-WHOLE-F# or Gb-WHOLE-G# or Ab-HALF-A-WHOLE-B-WHOLE-C# or Db-WHOLE-D# or Eb-HALF-E.

So the ‘ Do-Re-Mi etc’ scale starting at C is:

• C-D-E-F-G-A-B

and the ‘ Do-Re-Mi etc’ scale starting at E is:

• E-F#-G#-A-B-C#-D#-E (I left the ‘b’ names away to make it more clear, so only the  ‘#’ names here)

Since the name ‘ Do-Re-Mi etc scale’ doesn’t sound very professional. musicians call this scale ‘the Ionian’ scale.
So from now on, we call the scale with the formula ‘W-W-H-W-W-W-H’ the Ionian scale.

With the help of this formula, we can make an Ionian-scale for every note. So when someone says ‘Ionian in E’, you know that according to the Ionian-scale formula, this scale contains the following notes:

• ‘E-F#-G#-A-B-C#-D#-E’

The Chord

So we constructed a scale. A scale is just a string of separate notes but what if we would play two or more of these notes at the same time? That might sound OK as well.

Musicians have been experimenting for years with note combinations. That’ s fantastic since it enables us to use all the knowledge they built up. It appears that when you play the first, third and fifth note from a Ionian scale together, you get a magnificent sounding voice.

So for E-Ionian play the E-G#-B at the same time.<wav>
The same you can do for C-Ionian: C-E-G… also nice. <wav>

A chord with this construction (the 1st, 3rd and 5th from the Ionian scale) is called a Major chord. Major comes from the Italian word for big. I will explain later why we call these chords ‘Major’.

E-major has notes E-G#-B

Somebody else found out that if you lower the 3rd note one step, the chord sounds about the same but somehow a little bit ‘sad’. For this chord, you get the formula 1-3b-5 (b means lower a half step, so on the guitar one position down. For E-Ionian that means that the chord becomes: E-G-B. The ‘minor’ (small) chord was born.

Be aware that the E-Ionian scale doesn’t contain this lowered 3rd, the ‘G’ note is not in the E-Ionian scale. So it appears that we bumped into something new?

Scale chords

Building from what we have just learned we pick a random Ionian scale. Let’s pick D:

• D-E-F#-G-A-B-C#-D

according to the simple  formula: 1 – W – 2 – W – 3 – H – 4 – W – 5 – W – 6 – W – 7 – H – 8.

Looking from the first note (the D), ‘its’ (the D’s) third note (F#) has an interval of two whole notes. Have a look at your guitar, the D is on the 10th fret of the E-string, the F# on the 14th. Four (14-10=4) positions make two whole notes. This two whole notes, or four guitar positions, is always Major.

But looking in the same scale from the second note (E), the interval between the E and the E’s third note (the G) is only van 1,5 note, and that’ s minor! Check it on your guitar, the distance between the E and the G is three positions.

Looking from the third note (F) to his third is again 1,5 note (so minor), from the 4th (G) becomes major (2 whole notes) and the same is valid for the 5th (A). The 6th is minor. This leads to the following scheme:

• From the 1: major;
• From the 2: minor;
• From the 3: minor;
• From the 4: major;
• From the 5: major;
• From the 6: minor;

(The 7th is more complex and will be explained later)

When you apply this to the D-Ionian scale, you get the following “D-Ionian-own chords”:

• D major
• E minor
• F# minor
• G major
• A major
• B minor.

This gives us the basic foundation for pop music! These chords always sound good together. Give it a try, hit a random sequence of these chords and you will play a song. (If you have an iPhone or iPad, download the ‘Garage Band’ app. You can play keyboard and guitar chords according to this theory).

Some terminology. When you move from any given note to the third note, this is called a ‘triad’. So from our example of the D-ionian scale, the F# is the triad of D and is for example the A the triad of F#.
Play both combinations on a guitar (high e-string: 10th-14th and 2nd-5th fret). One ‘ triad’ has 4 fret spaces in between and the other has only 3.

They are both called triad but because these intervals have a complete different sound it is very important to be able to distinguish between the both of them. The triad with 4 fret spaces in between (or 2 whole notes) is called the ‘big triad’. The triad with 3 fret spaces in between or 1.5 note is called ‘small triad’.

• How is a major chord always built: keynote – big triad – small triad.
• How is a minor chord always built: keynote – small triad – big triad.

The whole chord theory is built around triads, always these same odd (in the meaning of not even) combinations. Therefore the official definition of a chord is the harmony of at least two triads. It’s important to realize what that means.

It must be clear as well where major and minor comes from, one starts with a major triad, the other one starts with a minor triad.

Extension of chords

What will happen if we add the next triad, which will be the 7th note from the scale? We’ll get a major 7th chord.

Looking at the Ionian D scale:

• D-E-F#-G-A-B-C#-D

According to the simple formula: 1 – W – 2 – W – 3 – H – 4 – W – 5 – W – 6 – W – 7 – H – 8:

• First: D-(2)-F#-(1.5)-A-(2)-C#: D major 7;
• Second: E-(1.5)-G (2)-B-(1.5)-D: E minor 7 (whole note between the 7th step from E, being the D and the E)
• Third: F#-(1.5)-A-(2)-C#-(1.5)-D: F# minor 7 (whole note between the 7th step from F#, being the E and the F#)
• Fourth: G-(2)-B-(1.5)-D-(2)-F#:  G major 7 (half note between the 7th step from G, being the F# and the G)
• Fifth: A-(2)-C#-(1.5)-E-(1.5)-G:  A 7 (whole note between the 7th step from A, being the G and the A)
• Sixth: B-(1.5)-D-(2)-F#-(1.5)-A :B minor 7 (whole note between the 7th step from B, being the A and the B).

Chord rule:
From the above overview you can deduct the following rules:

• the 1st and 4th are always major 7
• the 2nd, 3rd and 6th are always minor 7
• the 5th is always “dominant” septime

That third one, the “dominant septime” has this name for a specific reason. It is so dominant, it draws all the attention to itsef. Just play a  D major and then a A7. The  A7 chord is giving a weird feeling. We can even explain this feeling, the 7the step (with D-ionian the C#) “is begging” to finish the octave. This is the “unsatisfying feeling” you also hear when you play.

• C-D-E-F-G-A-B <wave>

Your ears beg you to play the C

It is important the learn the basic shapes of these chords by heart. Most probably you already know them. The best is to learn the E-shape (the ‘root’ on the low E-string) and the A-shape (root on the A-string):

 

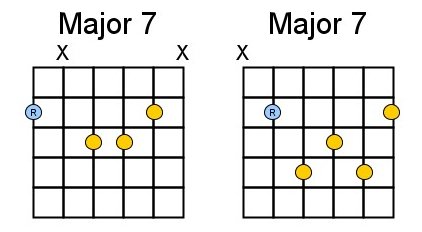
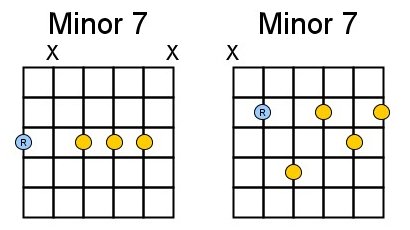
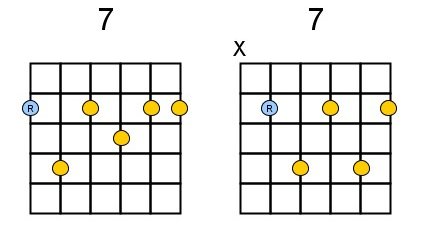
As we learned in the previous chapter, we were able to play all chords of a given scale randomly. We can also do that with 7th chords although you should be careful with playing the dominant 7, it only sounds good at certain places in your song. When, we’ ‘ll see later. But give it a try.

 

Scales – part 2

We”ll go back to the scales. From the different notes of the Ionian scale (do-re-mi) we have been constructing chords, but we can also construct different scales (yes, we can construct scales from a scale):

Looking at the Ionian D scale:

• D-E-F#-G-A-B-C#-D

Starting from the first note: D-E-F#-G-A-B-C# -D
Starting from the second note: E-F#-G-A-B-C# -D-E
Starting from the third note: F#-G-A-B-C# -D-E-F#
etc.

Those scales have different names
a) from the 1st: Ionian;
b) from the 2nd: Dorian;
c) from the 3rd: Frygian;
d) from the 4th: Lydian;
e) from the 5th: Mixolydian;
f) from the 6th: Aeolian;
g) from the 7th: Locrian.

So these are scales that consist of the same note-collection of 7 notes. The only differ from each other because they start from a different note.

When you assemble the rules, you get the following:

a) Ionian/major 7;
b) Dorian/minor 7;
c) Frygian/minor 7;
d) Lydian/major 7;
e) Mixolydian/dominant 7;
f) Aeolian/minor 7;
g) Locrian/(being ignored for now).

We always left out the 7th combination (Locrian scale, chord), I’ll show you why.

Let’s get back to the Ionian scale in D:
D-E-F#-G-A-B-C# -D, according to the simple formula: 1 – W – 2 – W – 3 – H – 4 – W – 5 – W – 6 – W – 7 – H – 8

When we apply our chord theory (1st, 3rd and 5th tone from the scale) And we look at the tone distances between the 1st, 3rd and 5th, we see::

• D major; D (2) F# (1.5) A
• E minor; E (1.5) G (2) B
• F# minor; F# (1.5) A (2) C#
• G major G (2) B (1.5) D
• A major; A (2) C# (1.5) D
• B minor. B (1.5) D (2) F#

A major chord: grote triad (2 notes or 4 fret positions) + small triad (1.5 note or 3 fret positions)
A minor chord: small triad (1.5) + big triad (2)

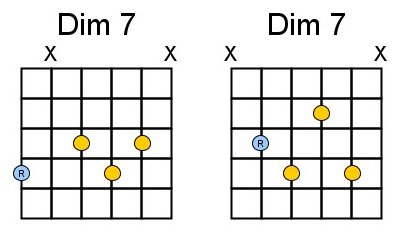
But now the C#, we get the C# (1.5) E (1.5) G. Our major/minor theory can’t be applied here, we found a new type of chords. A type of chord for which the distance between the 1st-3rd and 3rd-5th note are both a ‘small triad’ or 1,5 note or 3 fret positions,
These chords are indicated with “°”, in this example a C#° (C# diminished triad).

We can combine this with the 7th note. We get the following E and A-shapes:

 

 

We laid the fundamentals for chords and scales. We haven’t used them yet but you should be able by now to understand and explain how chords and scales are constructed.
Basically this is about 80% of the theory knowledge you must learn, so you have mastered even more than only the fundamentals.

Our next step is to see how chords interact with each other, the basis of music. Then we have a look at how the scales interact with chords, a must when you want to play solo’s over chords.

And to be honest, the previous part was the hardest part, so if you mastered the above…..

 

The circle of fifths

Now for something that you often find in theory books but is sometimes hard to grasp, the so-called circle of fifths.
Let’s go back to the original splitting op of the octave in eleven parts and we start at C:

C, Dd, D, Eb, E, F, Gb, G, Ab, A, Bb, B, C

We construct the Ionian scale:

C, D, E, F, G, A, B

We already had a look at the triad, the distance between two notes for which we have two possibilities:

• the small triad: this one has 2 notes with a distance of 1.5 note
• the big triad: this one has 2 notes with a distance of 2 notes

The fifth  is about 4 notes distance (the 5th note measured from the note where you start from).

The fifth of C is :

C,  D,  E,  F,  G,  A,  B
(1) (2) (3) (4) (5) (6) (7)

G. Have a look at the note distances:
C-D: 1 whole note
D-E: 1 whole note
E-F: half note
F-G: 1 note
————— +
3.5 note

From whatever note you start, the fifth always has a distance 3.5 note. So there is no big or small fifth like with triads, the fifth is so-called ‘perfect’.

Lets write down fifth’s:
C – G

Now start from the G. The G Ionian scale is:
G, A, B, C, D, E, F#. So the fifth of G is D:

G – D

Now look at D-Ionian:
D-E-F#-G-A-B-C#-D

D-A

etc.

Y’ll end up with the following sequence:

C-G-D-A-E-B-F#-C#-G#-D#-A#-F

A smart guy (or girl) once made a picture of this sequence:

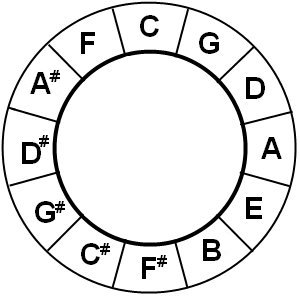
So turning clock-wise, you have the fifths of each note. But if you go in the other direction:

C-F

C,  D,  E,  F,  G,  A,  B
(1) (2) (3) (4) (5) (6) (7)

That’s a quart (4 steps)

F-Bb (of A#)

F-Ionian is:
F-G-A-A#-C-D-E

this interval also is a quart.

I think you can predict the outcome, going counter clockwise in the circle of fifths gives you quarts. A quart interval is always 2.5 note. As for fifths, quarts do not have big and small but are also ‘perfect’

OK, what is the practical use of this?

1. going clockwise or counter clockwise from one note to the next not on the circle of fifths is shiftable, the function doesn’t change. So going from C to D has the same function as going from A to E. In a popular way, it gives the same ‘feeling’. That’s handy when the singer in your band has a cold and can’t reach those high notes, you can ‘transpose’  the chords to for example a lower note by keeping the same ‘feeling’  in the music.

2. Although we calculated the circle of fifths with the help of the Ionian scale, the circle of fifths is applicable to all scales (based upon the 12 note division of the octave of course).

3. With the circle of fifth, you can easily determine what chords belong to a specific root. For example for C:

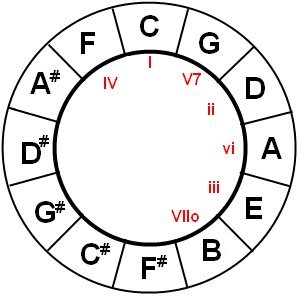
The notes with the Roman number indicate the used chords.

If you have a iPhone or iPad, buy the Garage band app. With the smart instruments tool you can make chord progressions based on this theory:

It’s a great tool to get introduced to the sound of these chords (except from playing the chords yourself of course).

Let’s go back to our list of chords from D-ionian:

• I   D major
• II  E minor
• III  F# minor
• IV  G major
• V  A7
• VI  B minor
• VII C#°

Shift all chord indications 2 to position clockwise and you’ll see that it fits perfectly with the chord sequence we calculated.

We continuously used the scale formula whole-whole-half-whole-whole-whole-half. We call this a major scale since the distance between the root and the 3rd note is two whole notes (the triad is a big triad).

But what will happen if me make the triad a small triad:
whole-half-whole-whole-half-whole-whole.

Then we get the (natural) minor scale (I cheated a little bit as you can see, I modified the formula not only for the triad but also for other notes. There are more minor scales, this one is called the natural and is widely used. You also have the harmonic etc.).

Let’s say, my root is C and I apply the natural minor scale formula to the C:

C-C#-D-D#-E-F-F#-G-G#-A-A#-B-C

then I get

C-D-D#-F-G-G#-A#-C
Compare this to the (Major) D# ionian scale.
D#-F-G-G#-A#-C-D-D#

These are exactly the same notes as in the C-minor scale. Only we start from a different note. Does that sound familiar? Scroll up, it’s the Aeolian scale.

This mapping of major and minor scales can be applied to all notes:

C major => A minor
G major=> E minor
D major=> B minor
etc.

Now our circle of fifths will look as follows. On the outside the major ‘tone’ and on the inside the corresponding (parallel) minor ‘tone’.

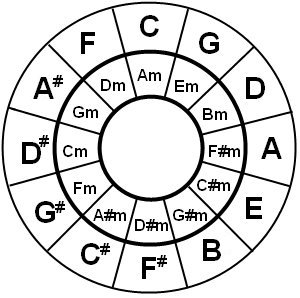
The notes that are connected to each other outside-inside (Like C and Am) are ‘exchangeable’. When we will study some songs, you will see that often these chords come in couples.

And now we had enough theory and is it time to put it all in practice. Based upon the knowledge presented above we can construct songs that sound nicely and comfortable. But as you might have seen when randomly playing chords ‘that belong to each other’, all chords have a typical feel or function.

We distinct the following functions:

The I chord, also called the ‘Tonic’, is the most important chord. When you depict a song as a voyage, this chord is your home. You leave from it and you return to it. In principle you don’t have to leave from it but the song is always drawn to this chord.

The most important chord after the I is the V, the ‘Dominant’. On your song-voyage, this chord says ‘go home’. Just play C – G7 – C (or I-V-I)…

The IV is called the ‘Subdominant’. Where the dominant orders you to go home, the subdominant wants you to enter the wide world, it draws you way from the Tonica. Example: C – F (I-IV).

The ii (in small printing since it’s a minor chord) is called the ‘Supertonic’. Super because it’s build one note above the Tonic. The ii often appears before the  V (dominant) that leads you to the I. The progression ii-V-I is by far the most important progression in jazz.
C-example: ii-V-I becomes Dmin – G7 -C.

The iii is called the ‘Mediant’, the chord (almost) in the middle. Also minor, in the C-example it’s the E minor. This chord doesn’t really have a role other then a substitute for other chords..

The vi is called ‘Submediant’. In C it is the A minor that is parallel to the Tonic (the I, so the C). So this chord can replace the I but it can also replace the IV.

Congratulations, you have mastered an enormous amount of musical theory. It’s not yet enough but it is a stable foundation for years of playing and studying.

I have applied this theory to some well known songs. Learn how to put this all in practice here!

And for those who want to have a more solid theoretical foundation, please check out this great video by the magnificent Pebber Brown. Its almost three hours long but worth every second!

Have fun !
Ed