“Western Music” – How did we end up with 12 notes?
We human beings (and probably animals as well) like to hear tones that have a specific frequency ratio. The frequency as you know is the number of vibrations for example a guitar string makes. If a guitar string makes 440 vibrations per second, it moves the air with this same frequency which is picked up by our ears. And we interpret this moving of the air as a tone. 440 Hz is fretting the high e-string at the 5th fret (A).
- High e: 329.63 Hz
- B-string 246.94 Hz
- G-string 196.00 Hz
- D-string 146.83 Hz
- A-string 110.00 Hz
- Low E-string 82.41 Hz
When you play two open strings at the same time, there is a ratio between the two frequencies. For example playing an Open (low) E string and the A string gives a ratio of 110/82.41 which is about 1.3333 (sorry, if you calculate it is 1.33478947 but lets assume it is a perfect 1.33333333). This is the ratio 4/3 because 4/3 is also 1.333333.
Do a check with the A and D-string (146.83/110=1.334818). Yes, we find the same ratio. It is valid for every consecutive string combination except for the G and B-string which have a ratio of 1.26.
In music theory we call this interval of notes a ‘perfect fourth’. In a regular tuning, the guitar strings are tunes in ‘perfect fourths’ except for the G-B string combination.
Back to the fact that we like to hear frequencies with a specific ratio. This was already discovered by the ancient Greek (historically this is attributed to the Greek philosopher Pythagoras). Story goes that Pythagoras passed a smith’s working place where the workers where hammering on two different pieces of metal. The sound the hammering sounded good together, something that Pythagoras noticed. But when he walked back (with a bag of calamaris) the workers were hammering on different pieces of metal and the combination sounded way off. Pythagoras got an idea, he decided to determine why two sounds sounded good together or sounded off.

So imagine that Pythagoras had two strings made of the same material with the same thickness and has them strung them with the same tension (the three variables the impact the frequency of guitar string tone are thickness, tension and length – on your guitar you have strings with different thicknesses, you can modify the tension with the tuning machines and you can vary the length by fretting a string).
These two strings would produce exactly the same tone. The frequency ratio between these strings is 1:1.
If one of these strings would be half the length of the other string, the two strings would produce different tones that sound in a way the same. The frequency ratio is 2:1.
and the list goes on.
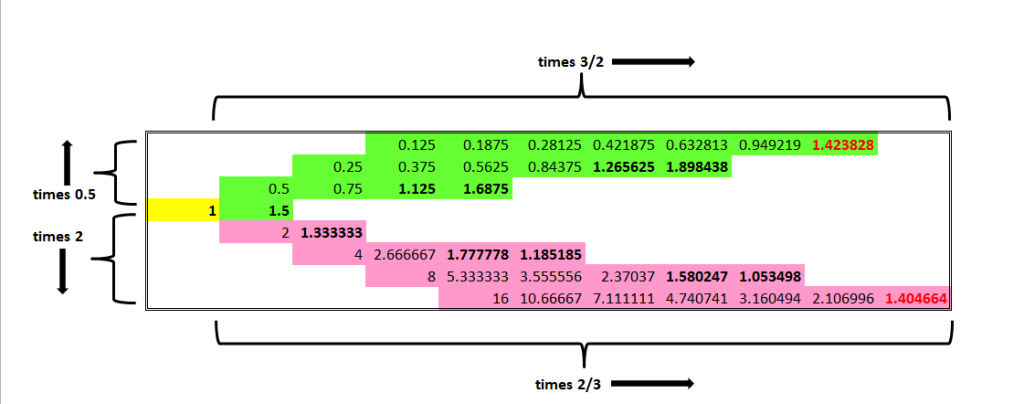
They don’t all sound as ‘good’. Sometimes you don’t hear that there are two strings (1:1 and 2:1 ratio) and some ratio’s sound ‘better’ then others. He particularly liked the 3:2 ratio. So let’s assume he did the following. He took a string of 1 meter, applied the 3:2 ratio to that string to calculate the string that would sound good together with this 1 meter string. This resulted in a string with length 66.6666 cm. On that string he would apply the 3:2 ratio again resulting in a 44.4444 cm string. On that 44.44 cm string he would apply the 3:2 rule again giving a 29.7 cm string etc. etc.
In order not to get too small strings – let’s say he wanted to have all strings between 1 and 2 meters length- he multiplied the string length by a multitude of 2. He did that because he learned that strings with ratio 2:1 can’t be distinguished from each other when they sound at the same time. So the 66,6666 cm string was made 1,3333 meters (2 times 66,6666 cm) and the 44,4444 cm string was made 1,7777 meters (2*2*44,4444).
The same he did the other way around, multiply instead of 2/3 the inverse factor of 3/2 to the 1 meter string resulting in a string of 1.5 meter (which has the 3:2 ratio with the 1 meter string). Apply the 3/2 factor to 1.5 giving a 2.25 meter string etc. etc. Again to fit between 1 and 2 meters length, he divided the resulting string length by a multitude of 2.
This results in what we now know as the Pythagorean tuning of 12 (ehhhhh 13, we will see later why). In an overview:
The bold values are the actual values to be used as string lengths. The red values will give Pythagoras (and us) an headache.
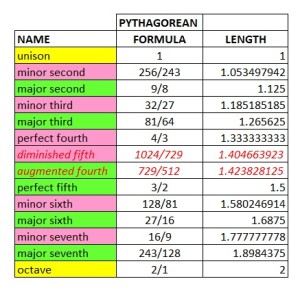
And listed in a table:
In the first column I have added the musical theory names of the intervals (see also my page on music theory). It’s just easy to use these names as a reference but I won’t explain the names here. You can see the mathematical formula in the second column as well. Taking a 1 meter string, multiplying it two times by 3/2 (or better 9/4) and then divide it by 2 gives formula 9/8, the third value in the list.
This set of string lengths (or notes) forms the basis for our modern 12-note tuning. As musicians were writing music and experimenting they found two big drawbacks of this tuning.
I already noted someting went wrong when working out the string lengths, it is related to the red values in our table. When using this way of calculating notes we find two notes – the diminished fifth and the augmented fourth – that should be the same but are in fact different notes. We call these notes ‘enharmonic’.
So we end up with 12 notes and something ‘extra’ of which we don’t know what to do with it. And we can’t ignore it because it makes our music sound ‘off’.
Although the 3:2 ratio’s sound perfect in this tuning, the other ratio’s like 4:3, 5:4 etc. are only possible (sound ‘good’) when you do them in combination with the 1 meter string.
Example: I want to test the 3:2 ratio with any value in the table. I take the ‘minor third’ (32/27=1.185185) and calculate the ratio with the ‘minor seventh’ (16/9=1.77777). These two should also have a ratio of 3:2. Well 1.7777777/1.185185185 gives 1.5! Perfect 3:2 ratio!
But now I want to test the 4:3 ratio. From the 1 meter string (‘unison’) that is the ‘perfect fourth’ or the exact 4:3 ratio (value 1.3333333). But this should also be the case when I take the ‘minor third’ (32/27) and the ‘perfect fifth’ (3/2). They should also have the 4:3 ratio but calculating this gives the result of 1.265625! Not even close to 1.3333333!
Both drawbacks are caused by the simple fact that no power of 2 can equal a value of power of 3.
In our calculations above we used powers of 2 and 3 to calculate the values of the string lengths.
Unison is 1 which is: 3^0/2^0 = 1 (anything to the power of 0 is 1)
Minor Second: 2^8/3^5
Major second: 3^3/2^4
major third: 2^5/3^3
etc.
Using the ratios of 2:1 and 3:2 doesn’t give a closed system. A gap will always exist: the ‘Pythagorean comma’.
The difference between those ranges (129,746-128) is the Pythagorean comma.
During hundred of years, musicians and scientist have come up with different methods of calculating intervals. There is a lot to find on the internet and it goes too deep to discuss this here. For now we leap from the ancient Greek to Holland in the 16th century.
In the 16th century, the Dutchman Simon Stevin had created a mathematical formula to divide a string in 12 logarithmic equal spaces. The tuning derived from this formula is called the ‘Equally Tempered’ tuning and has become the standard since the 19th century. In this tuning there are no exact ratio’s (3:2, 4:3 etc.) as there are in the Pythagorean tuning, but an important interval the perfect fifth (3:2) comes quite close. Let’s say, it’s all a little bit ‘off’ but you can use it, play different intervals in different keys and it all sounds fairly OK. For us it is important that this formula is used for guitar building and guitar tuning. The distances between the frets on your guitar are calculated based on Simon Stevin’s formula to divide an octave in 12 parts. You do this by dividing the string length (in our example 1 meter) by:
12√2 = 21⁄12 ≈ 1,059463
1/1,059463 gives 0,943874397. So your first fret will be at a distance of about 0.944 from the bridge (or 1-0,944=0,056 from the nut).
For the second fret you use the string length from the first fret 0,943874397. Divide this by 1,059463 and you get 0.8909 which is the distance of the second fret from the bridge.
In a formula: nth fret distance from the bridge = 1/2 n/12
You can repeat this 12 times and then you will end up exactly at half of the string because 1/2 12/12 = 1/2 = 0,5. The octave is divided in exactly 12 notes and not in 12 notes and ‘something’ as in the Pythagorean tuning!
As mentioned before, drawback of this method is that none of the intervals we ‘like’ (3:2, 4:3, 5:4 etc.) will be correct. In order to show this we need some extra theory and I promise you this is the last formula we will need.
We need to quantify the distance between notes somehow but in a way that the distance between notes doesn’t matter. So the distance between the minor second and the following note the major second must have the same ‘weight’ as for example between the minor sixth and the following note the major sixth. We define the distance between consecutive notes as ‘100 cent’ and since we have 12 notes, the ‘weight’ of an octave is 12 times 100 which is 1200 cents.
The formula to express the weight for any given combination of notes (frequencies) is: 1200 * 2 Log (f1/f2)
Where f1/f2 ratio between the frequencies of the different notes.
It is a difficult formula but it is very handy as we will see.
Example: we want to define the ‘weighted’ distance of a perfect 5th. From our formula this is 1200 * 2 Log (3/2) =701,955.
The ‘weighted’ distance of a octave is: 1200 * 2 Log (2/1) =1200 cents.
The ‘weighted’ distance of a perfect 4th is: 1200 * 2 Log (4/3) =498,045 cents.
Experiments have proved that the average human ear can only hear differences in notes that are higher than 5 cents. So a note that is 5 cents or less ‘out of tune’ sounds to most ears equal to the same note that is perfectly in tune.
These 5 cents gives us the possibility to add some length to one string or remove some length from another string, without hearing any difference. This can be very useful in solving most of our tuning problems.
In the 18th century, the German Andreas Werckmeister created a number of so-called ‘Well-tempered’ tunings which make use of this effect. By adjusting some notes within the +/- 5 cent range he was able to create tunings that had well sounding intervals (3:2, 4:3, 5:4 etc.) which could be used over all keys.
Werckmeister’s ‘Well-tempered tuning I’ was loved by Johann Sebastian Bach who also wrote specific musical pieces to demonstrate the capabilities of this tuning (check out ‘Das Wohltemperierte Klavier’, or the ‘Well-tempered piano’).
But imagine, these ‘Well-tempered tunings’ developed in the 18th century were not very scientific. They were just instructions how to manually adjust a standard tuning such as a Pythagorean tuning or any other tuning that had been developed. Simply because the needed mathematics and physics knowledge was not available. And just think of the absence of good measuring devices. There was no such thing as an oscilloscope in the 18th century, everything had to be done by ear.
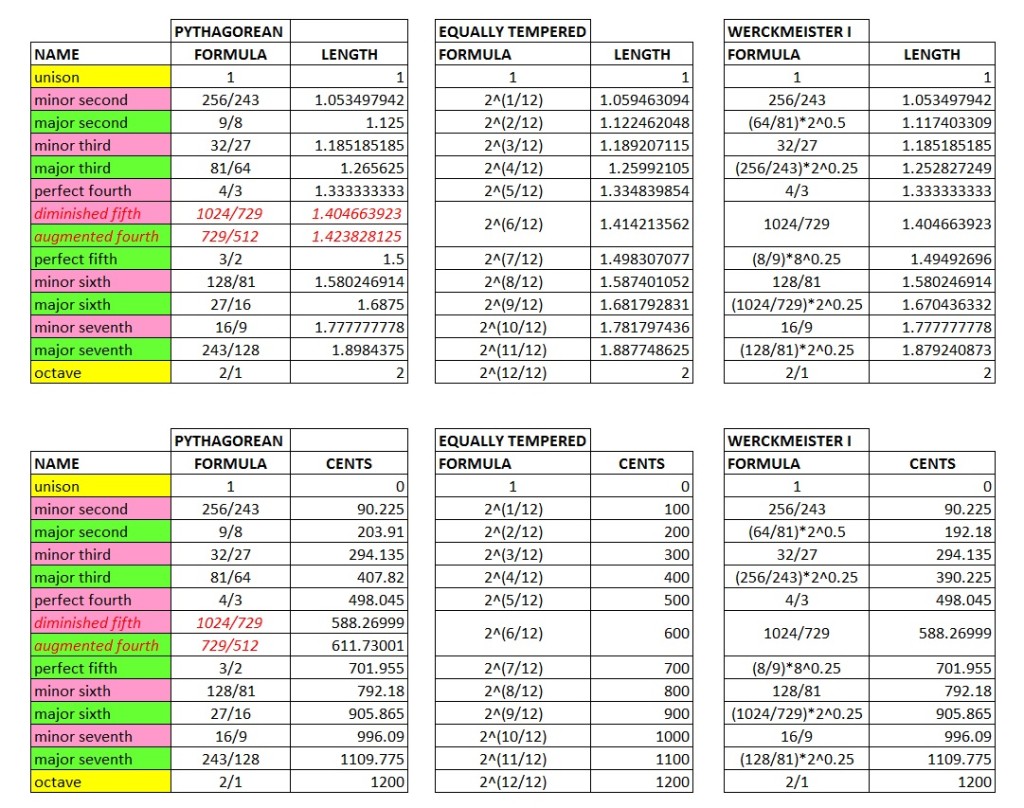
Let’s put the three different tunings we discussed (Pythagorean, Equally Tempered and ‘ Werckmeister I’ ) in one table together with the formula’s, lengths and cents:
- The Pythagorean tuning: fully based on octaves (2:1) and perfect fifths (3:2) but with the drawback that there is a ‘remainder’ and in other keys than the root key other intervals like 4:3 and 5:4 sound off.
- The Equally Tempered tuning: a very mathematical tuning in which there are no intervals that sound really ‘good’ or ‘off’. Usable for every key.
- The Werckmeister I tuning: basically the Pythagorean tuning adjusted so that it’s main drawbacks are compensated for.
OK you think, how is that related to my guitar?
Well, almost all (99.9%) of the guitars (we will see some exceptions later) are built using the ‘Equally Tempered’ tuning. When you tune your guitar with a tuner, the tuner ‘listens’ to the guitar’s sound and indicates how many cents the sound from your guitar is off from the ‘Equally Tempered’ tuning. And as we have seen, this tuning has not correct intervals, especially on the Major Third and Minor Third interval.
So you have tuned your guitar and you play an E Major chord just as everyone does. It sounds OK, the Major Third is off but you and the band members don’t hear or can’t hear it. Then you switch on your overdrive pedal and play the E-chord again. Now with all the overtones produced, the chord sounds awful. ‘Well’, you say, ‘ it’s that horrible G-string again’ so you adjust your G-string in such a way that your E-chord sounds well. And then you hit a G-chord….aauuugghhhhhhh, way off!
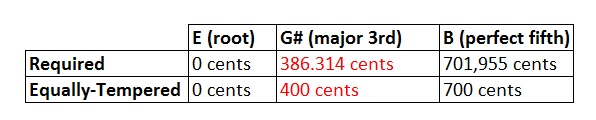
What happened? As explained above your frets are placed according to the ‘equally tempered’ formula and your strings are tuned according to that same formula. Playing an E-chord gives the following notes: E (root) – G# (major 3rd) – B (perfect 5th).
Well, the 5ths (on the A and B-string) are about 2 cents off, very hard if not impossible to hear, even with fuzz and overdrive. But the Major 3rd (on the G-string) is almost 14 cents off, way beyond our tolerance of 5 cents. You bet you are going to hear that specially with extra overtones produced by fuzz and overdrive.
When you decide to tune your G-string by ear based on the E major chord, you introduced a wrongly tuned string in your set-up. So when you play a G-chord, both the A-string (which is the Third) and the G-string (which is the Root) will sound off.
That’s why many rock and metal bands don’t play thirds, they play so-called power chords which only consist of a Root and a Fifth, both can be tuned well. Pythagoras must have been a heavy metal fan!
Besides this, the G-string is a problem child. It should be a wound string like jazz players often have. There is so much tension on this string that it’s hard keep in tune anyway.
The same is valid for an A-shaped chord. Here the major 3rd is on the B-string. Eddie van Halen used to tune his B-string a fraction down so the 3rd would sound much better. Think of songs like ‘Running with the devil’, ‘Panama’ etc. Eddie plays these A-shaped chord all over the neck with a perfectly sounding B-string. And because the major 3rd can be heard well it makes these chord sound ‘happy’ therefore van Halen’s music is often referred to as ‘happy metal’.
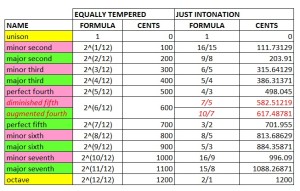
Those who checked the table above very well might ask themselves where the value of 386,314 cents comes from. This value can’t be found in the Pythagorean/Equally tempered/Werckmeister table? Well, as stated before, we like to hear specific intervals and these intervals are based on ratios of the smallest possible whole number. Intervals definition with these ratios is called ‘Just Intonation’ and we use these values as reference. If you map this to the equally tempered intervals you get the following table:
So what we really like to hear as intervals are the ‘Just Intonation’ intervals and what we hear when playing guitar are the ‘Equally Tempered’ intervals.
Well that’s about it. We had a brief look on how Equally Tempered tuning of our guitar has its flaws. But for us guitar players that’s not all. There are a few other issues that screw up our tuning:
- When we press a string behind a fret, there will be a little bit more tension on the string causing the note to go sharp
- Strings that are fretted always will have a little part of the string (right after the fret) that will not vibrate. This causes the string to be a little bit shorter causing the note to go sharp.
- Strings (especially new strings) will stretch.
- …..
We only can do our best by compensating for these effects by intonating our guitar. Please check my article on tuning and intonating.
And what are the options we have to fix all our guitar issues:
Earvana
Earvana offers a so-called compenstaed nut. As you can see in the picture below the G-string comes a little bit closer to the first fret which results in slighter higher pitched G-string. This sounds particulary good with thirds in E-shaped chords.

Also the B and A-string are compensated for. With the small screws it is possible to adjust the compensation a little bit. I have installed this on a Les Paul copy and I was not too impressed. Also the screws are very small and the fine adjustment is very hard to do (you need a strobe tuner and still then it’s very hard). I would not recommend this to install it yourself. If you like to try this out please visit a luthier that has experience with this system and do some tests on a guitar that has this nut installed.
Fretwave
Fretwave requires to replace the first and second fret with new frets that have a slight bow at the G-string (first fret) and a even slighter bow at the B-string (second fret). I only played once on a ‘fretwave’ guitar. This was a guitar built by Sander de Gier, a very talented luthier. He was very impressed by the results from the fretwave although he hardly sold it to customers. People tend to think it makes playing more complex but that is not the case.

As for the Earvana nut, the fretwave particulary fixes the third in a E-shape and A-shape (barré) chord.
Buzz Feiten
The Buzz Feiten system is maybe the most ‘invisible’ system. It mainly consists of two parts:
- A compensated nut
- Adjusted fret location

As I checked the Buzz Feiten website (www.buzzfeiten.com), I couldn’t find the ‘adjusted fret location’ anymore. This system I used for my ‘Billy Bo’ replica. The location of the frets is slightly different from the ‘equally-tempered’ fret location. Together with different fret locations also the guitar should be intonated differently, you need a special tuner which supports the Buzz Feiten tuning (like a Peterson Tuner or a Korg DT-7). The regular tuning of a guitar can be done with any regular tuner.
Some brands like Washburn offer this Buzz Feiten fret location system as default for all of their guitars and it’s really an improvement. But why don’t other brands use this? Well the main reason is that the Buzz Feiten system costs a specific license fee (for my Billy Bo project built it was about $60) and for most brands that is to costly also for their expensive models. It’s rumoured that Joe Satriani’s personal guitars have the Buzz Feiten fret location system but his Ibanez production models definately dont’ have it.
On the Buzz Feiten website I could only find the compensated nut system. I don’t know the details but it looks like an Earvana kind of nut together with some intonation hints.
Well-tempered necks
Not that long ago I bumped into a Swedish company that offers of so-called ‘true-temperament’ necks. So a kind of ‘Werckmeister’ necks. Check out their website www.truetemperament.com.

I never played one but I am very curious. I remember this company used to offer different ‘temperaments’, for example a neck more suited to play rock chords or a neck more suited to play jazz chords. But nowadays I can only find one type of neck.
Necks are bout 6000,- Swedish krona (excl freight costs and any taxes) which is about $750,- so they don’t come cheap.
Hope you liked this article. To be honest, maybe it is not all 100% correct but I did my best to make it as readable and non-technical as possible.
Other sources:
http://leware.net/temper/temper.htm
http://www.medieval.org/emfaq/harmony/pyth.html